こんにちはの方もこんばんはの方もようこそ、イカスミです。
大学生、特に情報系学生の皆さん、決定性有限オートマトンはわかるけど、非決定性有限オートマトンって何?となった経験はありませんか?
この記事では、そんな方に向けて、現役理系大学生の僕が、決定性有限オートマトンについて解説したいと思います。
この記事で解決できる悩み
- 非決定性有限オートマトンがわからない
- 非決定性有限オートマトンの問題が解けない
非決定性有限オートマトンとは?
決定性有限オートマトンとは、1つの入力に対して、遷移する状態がただ1つ決まっているオートマトンでした。
非決定性有限オートマトンとは、ある1つの状態に入力を行ったとき、遷移先の状態が複数存在するオートマトンのことを指します。
アルファベットで、NFA(の略)と呼びます。
数式表現や状態遷移図については、DFAと同様です。
例題をわかりやすく解説
0と1から成る文字列のうち、末尾が1の言語 を受理するNFAの状態遷移図を求めましょう。
まず、受理状態を考えると、末尾が1なので、直前の入力が1で、かつその入力が最後である状態を用意します。
次に、開始状態を考えます。
受理状態に遷移するときは1を入力するので、開始状態からは1を読みます。
よって、状態数は2つでよいとわかります。
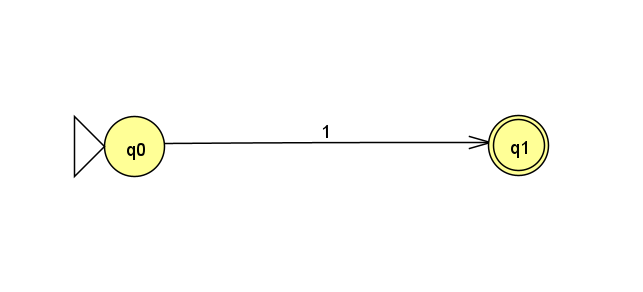
開始状態には0と1のどちらを読んでも、開始状態に戻るように遷移します。また、1を読んだ場合、もう1つの遷移先として受理状態を用意します。
最終的な状態遷移図は、このようになります。
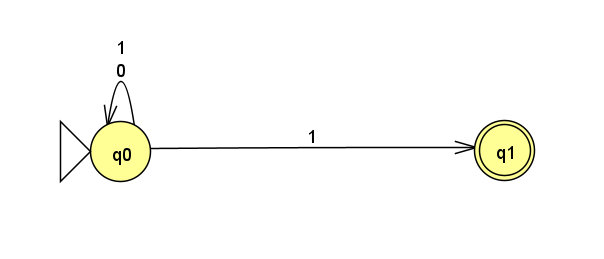
DFAで表現すると?
DFAで表現した場合、状態遷移図はこのようになります。
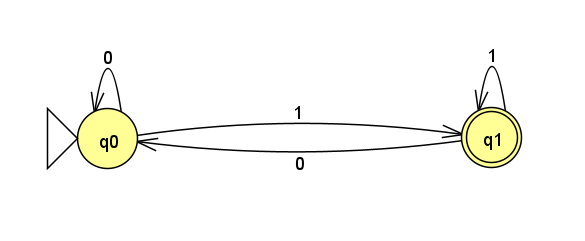
状態数はNFAと同じですが、遷移の様子が違います。
0を読むと開始状態に、1を読むと受理状態に遷移します。
NFAとは異なり、遷移先が1つしかないことがわかります。
演習問題
問題1
末尾が01の文字列を受理する言語について、NFAの状態遷移図を与えよ。
問題2
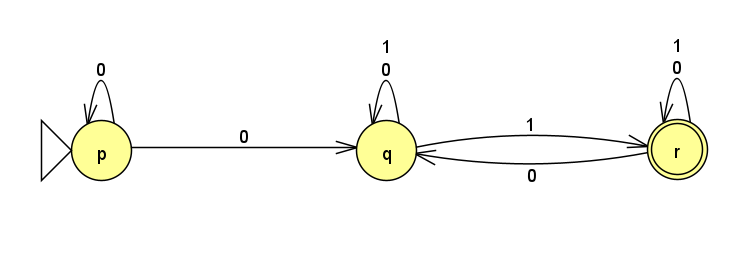
以下の式状態遷移表で与えられるNFAの状態遷移図を求めよ。(→は開始状態、*は受理状態)
| 0 | 1 | |
| →p | {p, q} | Φ |
| q | {q} | {q, r} |
| *r | {q, r} | {r} |
解答
問題1
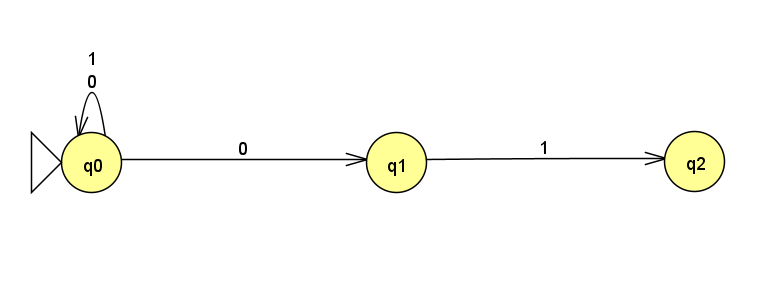
0 ⇒ 1という入力で終われば入力が受理されるので、まず、開始状態から、0 ⇒ 1と読み、2つの状態を経て受理状態に遷移するようにします。
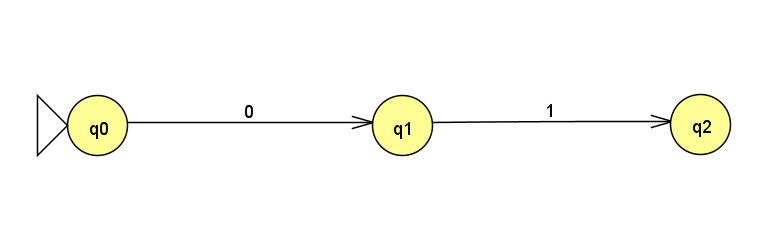
末尾の01より前の部分列は、開始状態での遷移で作ればいいので、最終的な状態遷移図は、このようになります。
問題2
まとめ
この記事でわかったことは、
- 非決定性有限オートマトンは、ある入力に対して、遷移する状態が複数存在する
- 状態遷移図の作り方は、決定性有限オートマトンと変わらない
最後まで読んで頂き、ありがとうございました。