こんにちはの方もこんばんはの方もようこそ、イカスミです。
大学生、特に情報系学生の皆さん、形式言語の授業で、決定性有限オートマトンって何?となった経験はありませんか?
この記事では、そんな方に向けて、現役理系大学生の僕が、決定性有限オートマトンについて解説したいと思います。
この記事で解決できる悩み
- 決定性有限オートマトンがわからない
- 決定性有限オートマトンの問題が解けない
有限オートマトンとは?
オートマトンとは、簡単に言うと、状態と、状態を変化させる規則である遷移関数によって表されるモデルのことを言います。数式表現、状態遷移図の2種類の表現方法があります。
また、有限オートマトンには、決定性有限オートマトン・非決定性有限オートマトンの2つが存在します。
決定性とは、1つの入力に対して、遷移先の状態が1つであるオートマトンのことです。
対して、非決定性とは、 1つの入力に対して、遷移先の状態複数選べるオートマトンのことを指します。
決定性有限オートマトンをわかりやすく解説
決定性有限オートマトンとは、ある1つの状態に入力を行うと、遷移先が必ず1つに定まっているオートマトンのことです。
アルファベットではDFA(deterministic finite automaton の頭文字の略)と呼びます。
数式による定義では、
DFA = (Q, Σ, δ, q0, F)
と表され、それぞれの記号は
Q:状態の集合
Σ:入力の集合
δ:遷移関数
q0:開始状態
F:受理状態
を表します。
その他に、状態遷移図で表す方法があります。
例えば、下のような状態遷移図が考えられます( JFLAPというツールを利用)。このオートマトンは、0と1から成る文字列のうち、部分列として(文字列の途中に)01を含む言語 を受理します。
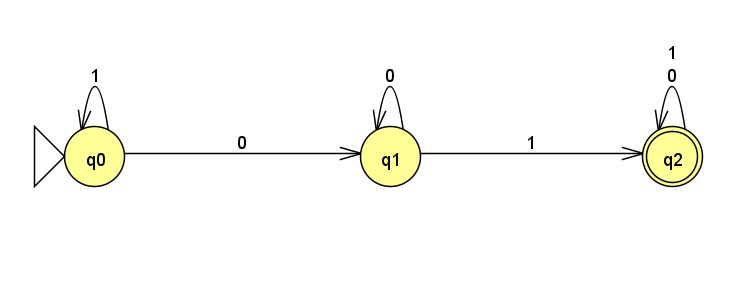
アルファベットが付けられたそれぞれのマークは、状態を表します。
→で、入力と遷移方向を表します。
開始状態には→を付け、受理状態は◎で表します。
開始状態は1つだけですが、受理状態は複数設定することが可能です。
このようにして表す図を、オートマトンの状態遷移図と呼びます。
3つの状態q0、q2、q3は、それぞれ
- q0:入力が何もない、または直前の入力が1である状態 (開始状態)
- q1:直前の入力が0である状態
- q2:直前の入力が0である状態 (受理状態)
を表します。
入力が101の場合、1 → 0 → 1 というように入力が状態に渡されます。
最初の状態はq0なので、1を入力しても状態はq0のままです。次の入力の0では、状態がq0からq1へと遷移します。最後に1を入力すると、状態が q1からq2へと遷移し、受理状態になったので、入力が受理されます。
ここからさらに入力しても、q2から他の状態に遷移することはないので、 入力は受理され続けます。
入力が110の場合、最終的な状態がq2で止まってしまうので、入力は受理されません。
実際に入力してみると、

101が受理され、110が受理されないことがわかります。
数式として表現すると、
({q0, q1, q2}, {0, 1}, δ, q0, {q2}), δ(q0, 0) = q1, δ(q0, 1) = q0, δ(q1, 0) = q1, δ(q1, 1) = q2, δ(q2, 0) = q2, δ(q2, 1) = q2
問題を解いてさらにわかりやすく
それでは、さらに理解を深めるために、問題を解いて行きましょう。
例題
言語Lを、L = {ω | ωは偶数個の0と偶数個の1を含む} と定義する。
言語Lを受理するDFAの状態遷移図を求めよ。
解説
偶数個の0と1を含むので、まずは0と1の個数によって状態を分ける必要があります。
入力は0か1、個数は偶数か奇数なので、状態は全部で4つ必要だとわかります。
- q0:それまでに読んだ0と1の個数は共に偶数である (開始状態、受理状態)
- q1:それまでに読んだ0の個数は奇数で、1の個数は偶数である
- q2:それまでに読んだ0の個数は偶数で、1の個数は奇数である
- q3:それまでに読んだ0と1の個数は共に奇数である
よって、状態遷移図はこのようになります。
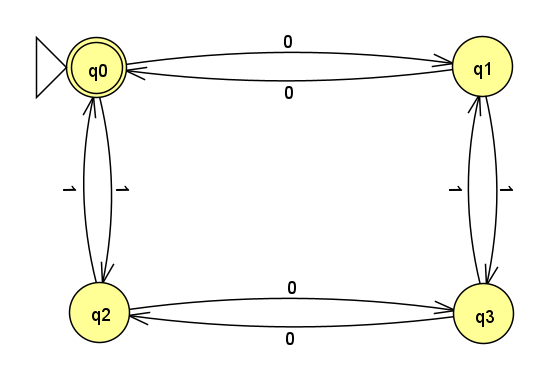
演習問題
問題1
0と1から成る文字列のうち、部分列として101を含む言語を受理するDFAの状態遷移図を求めよ。
問題2
L = {w | ωは偶数個の0と奇数個の1を含む} について、言語Lを受理するDFAの状態遷移図を求めよ。
問題3
L = {w | ωは0を3の倍数個含む} について、 言語Lを受理するDFAの状態遷移図を求めよ。
※ヒント
自然数は、3で割ったときの余りが0の数、1の数、2の数に分けられます。ということは、必要な状態は・・・ (0は余り0!)
解答
問題1

問題2
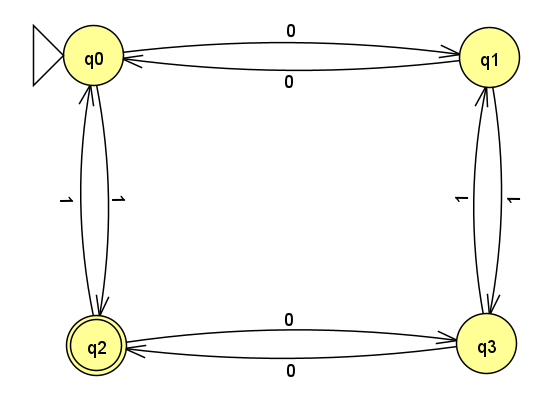
問題3
必要な状態は、
- q0:それまでに入力された0は3n個である (n >= 0, 開始状態、受理状態)
- q1:それまでに入力された0は(3n + 1)個である
- q2:それまでに入力された0は(3n + 2)個である
なので、状態遷移図は、
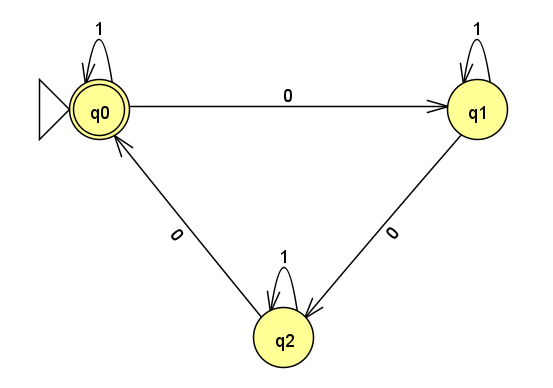
まとめ
この記事では、
- 決定性有限オートマトン
- 決定性有限オートマトンの問題の解き方
を解説しました。
この記事を読んで、決定性有限オートマトンについての理解が深まれば幸いです。
最後まで読んで頂き、ありがとうございました。