こんにちはの方もこんばんはの方もようこそ、イカスミです。
大学生、特に情報系学生の皆さん、形式言語の授業で、チューリングマシンって何?となった経験はありませんか?
チューリングマシンは、形式言語などの授業では特に重要なので、理解することが必要です。
この記事では、情報系大学生の僕がチューリングマシンについて解説したいと思います。
この記事で解決できる悩み
- チューリングマシンがわからない
- チューリングマシンをどう設計すればいいのかわからない
この記事では、この参考書を基準にしているので、余裕がある方は手にとってみてください。
チューリングマシンとは
チューリングマシンは、1936年に、イギリスの数学者であるアラン・チューリングが考案したモデルで、コンピュータを模倣する能力を持ちます。
この「コンピュータを模倣する」という能力が非常に重要なのですが、この記事では深く取り扱いません。
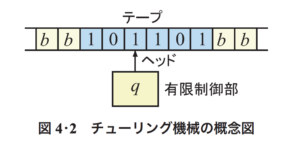
チューリングマシンには、テープと呼ばれる記憶装置があります。
有限オートマトン + テープと考えるとわかりやすいです。
テープには、それぞれのマスに入力が置かれ、テープヘッドを左右に動かすことで入力を読んでいきます。
テープの他のマスは、空白記号を表します。
図で示すと、このようになります。
引用元:[補足] チューリングマシン
そして、チューリングマシンは1回の動作で、次の操作を行います。
- 状態を変える。状態は、現在の状態でもいい。
- 読んでいるマスの記号を書き換える。記号は、現在の記号と同じでもいい。
- テープヘッドを右か左に動かす。
テープヘッドが示すマスの記号を変え、ヘッドを動かす。
この考え方が、非常に重要になります。
有限オートマトン・プッシュダウンオートマトンとの違い
チューリングマシンにはテープがあるので、有限オートマトンよりも表現できる言語は多くなります。
プッシュダウンオートマトンにもスタックという記憶装置がありますが、スタックは先入れ後出しでしか情報にアクセスできません。
しかし、チューリングマシンはテープヘッドを動かすことでどのマスにも移動できるため、計算能力はチューリングマシンに軍配が上がります。
有限オートマトンとプッシュダウンオートマトンについては、こちらの記事で解説しています。
-

-
【現役大学生が決定性有限オートマトンをわかりやすく解説します】形式言語とオートマトン
こんにちはの方もこんばんはの方もようこそ、イカスミです。 大学生、特に情報系学生の皆さん、形式言語の授業で、決定性有限オートマトンって何?となった経験はありませんか? この記事では、そんな方に向けて、 ...
続きを見る
-

-
【現役大学生が非決定性有限オートマトンをわかりやすく解説します】形式言語とオートマトン
こんにちはの方もこんばんはの方もようこそ、イカスミです。 大学生、特に情報系学生の皆さん、決定性有限オートマトンはわかるけど、非決定性有限オートマトンって何?となった経験はありませんか? この記事では ...
続きを見る
-

-
【情報系大学生がプッシュダウンオートマトンをわかりやすく解説】形式言語とオートマトン
こんにちはの方もこんばんはの方もようこそ、イカスミです。 大学生、特に情報系学生の皆さん、形式言語の授業で、プッシュダウンオートマトンって何?となった経験はありませんか? この記事では、そんな方に向け ...
続きを見る
例題を用いてわかりやすく解説
例題として、この問題を考えます。
例題:言語 L = {0n1n|n = 0, 1, 2. ・・・} を受理するチューリングマシンを設計せよ。
このチューリングマシンで使う記号は、0, 1, X, Y, □ の5つです。
0と1は入力記号、XとYはテープでの置き換え用の記号、□は空白記号となります。
では、チューリングマシンを設計していきましょう。
まずは、入力をテープに置きます。
このとき、テープヘッドは入力の先頭を示しています。
以降は、入力の左端から次の動作を行い、入力を読み込んでいきます。
-
テープヘッドが示している記号0を読み、Xに変える。
-
1に出会うまで、0やYを読み飛ばしながらテープヘッドを右に動かす。
-
テープヘッドが示している記号1を読み、Yに変える。
-
Xに出会うまで、0やYを読み飛ばしながらテープヘッドを左に動かし、テープヘッドをXの1マス右隣に動かす。
- ①~④の動作を繰り返す。
以上の操作を繰り返し、テープの入力列がXnYnに変わっていれば、入力が受理されます。
では、これを状態遷移図にしてみましょう。
状態遷移図は、このようになります。
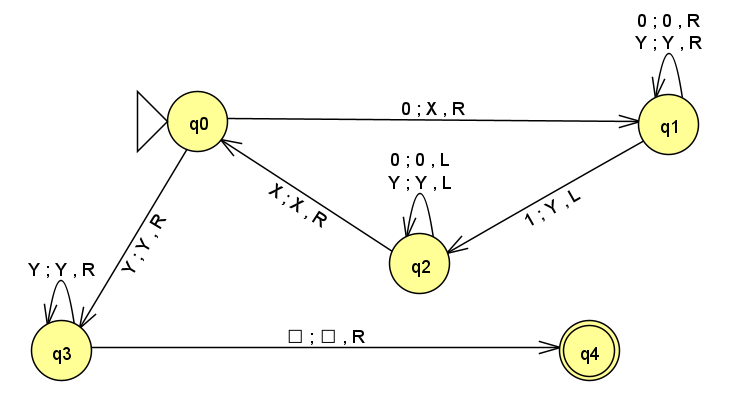
①から⑤の動作が、上手く表現できています。
入力がXnYnに変わっている場合、q0→q3→q4と遷移し、入力が受理されます。
入力の0が1よりも少ない場合、入力はXmYm1n-m ( m < n )に変化し、q0→q3と遷移しますが、1が変化せずに残っているので、空白記号に出会うことができません。
そのため、q4に遷移せず、入力は受理されません。
入力の0が1よりも多い場合、入力はXm0n-mYm (m < n)に変化し、最終的にq1で1ではなく空白記号に出会ってしまい、入力は受理されません。
状態遷移図を用いると、理解しやすくなると思います。
まとめ
この記事では、チューリングマシンについて解説しました。まとめると、
- チューリングマシンは、有限オートマトンにテープを付け加えたもの
- 1回の動作で、マスの読み込み・現在読んでいる記号の変更・テープヘッドの移動 を行う
この記事が、皆さんの学習の参考になれば幸いです。
最後まで読んで頂き、ありがとうございました。